[문제 설명]
좌표평면을 좋아하는 진수는 x축과 y축이 직교하는 2차원 좌표평면에 점을 찍으면서 놀고 있습니다. 진수는 두 양의 정수 k, d가 주어질 때 다음과 같이 점을 찍으려 합니다.
원점(0, 0)으로부터 x축 방향으로 a*k(a = 0, 1, 2, 3 ...), y축 방향으로 b*k(b = 0, 1, 2, 3 ...)만큼 떨어진 위치에 점을 찍습니다.
원점과 거리가 d를 넘는 위치에는 점을 찍지 않습니다.
예를 들어, k가 2, d가 4인 경우에는 (0, 0), (0, 2), (0, 4), (2, 0), (2, 2), (4, 0) 위치에 점을 찍어 총 6개의 점을 찍습니다.
정수 k와 원점과의 거리를 나타내는 정수 d가 주어졌을 때, 점이 총 몇 개 찍히는지 return 하는 solution 함수를 완성하세요
[접근 방법]
문제를 이해만 하면 풀이는 아주 쉽습니다. 즉 (a*k, b*k)의 길이가 d보다 작으면 된다는 말입니다.
학교 다닐 때 많이 외웠던 공식 중 하나인 대각선 길이 구하는 공식...
a^2 + b^2 <= d^2
이걸 알고 있냐 모르냐 묻는 문제라고 생각해도 될 것 같네요.
[1차 시도]
class Solution {
public long solution(int k, int d) {
int answer = 0;
int max = d/k+1;
int[] xy = new int[max];
for (int i=0; i<max; i++) {
xy[i] = i*k;
}
for (int a=0; a<max; a++) {
for (int b=0; b<max; b++) {
double dis = Math.sqrt(Math.pow(xy[a], 2)+Math.pow(xy[b], 2));
if(dis<=(double)d) {
answer++;
}
}
}
return answer;
}
}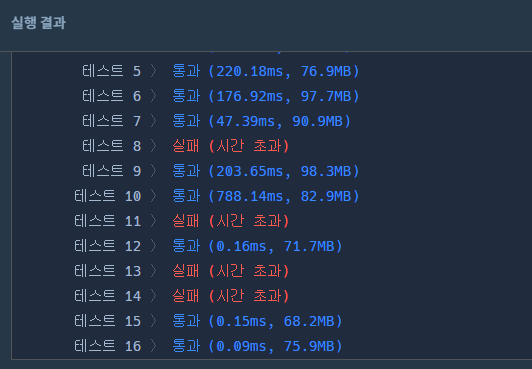
이제는 익숙한 빨간색 시간 초과. 문제 자체는 쉬운 대신 이중 for문을 쓰면 얄짤 없이 시간 초과가 납니다.
이중 for 문을 줄이려고 생각해보니 한 좌표로 해결해야 할 것 같습니다.
b^2 <= d^2 - a^2
수식을 보면 알고 있는 값이 두 가지 있네요. a 좌표와 d 값을 알고 있으니 b 좌표만 구하면 되겠습니다.
[정답]
class Solution {
public long solution(int k, int d) {
long answer = 0;
for (long a=0; a<=d; a+=k) {
long b = (long)(Math.sqrt(Math.pow(d, 2)-Math.pow(a, 2)));
answer += b/k+1;
}
return answer;
}
}'코딩 테스트' 카테고리의 다른 글
| [프로그래머스] PCCP 기출문제 2번 석유 시추 (LV.2/JAVA) (2) | 2024.12.17 |
|---|---|
| [프로그래머스] 호텔 방 배정 (LV.4/JAVA) (0) | 2024.08.12 |
| [프로그래머스] 달리기 경주 (LV.1/JAVA) (0) | 2024.06.10 |
| [프로그래머스] 롤케이크 자르기 (LV.2/JAVA) (0) | 2024.03.01 |
| [프로그래머스] 귤 고르기 (LV.2/JAVA) (0) | 2024.03.01 |
